Histogram of Results

ggplot(data.frame(weeks = weeks_to_athena_items), aes(x = weeks)) + 
  geom_histogram(bins = 50, fill = "purple", color = "black", alpha = .5) + 
  geom_vline(xintercept = average_weeks) +
  labs(title = "Distribution of Weeks to Get All 6 Items",
       subtitle = "Assumes all items have equal probability in any week",
       x = "Weeks",
       y = "Count") +
  theme_light()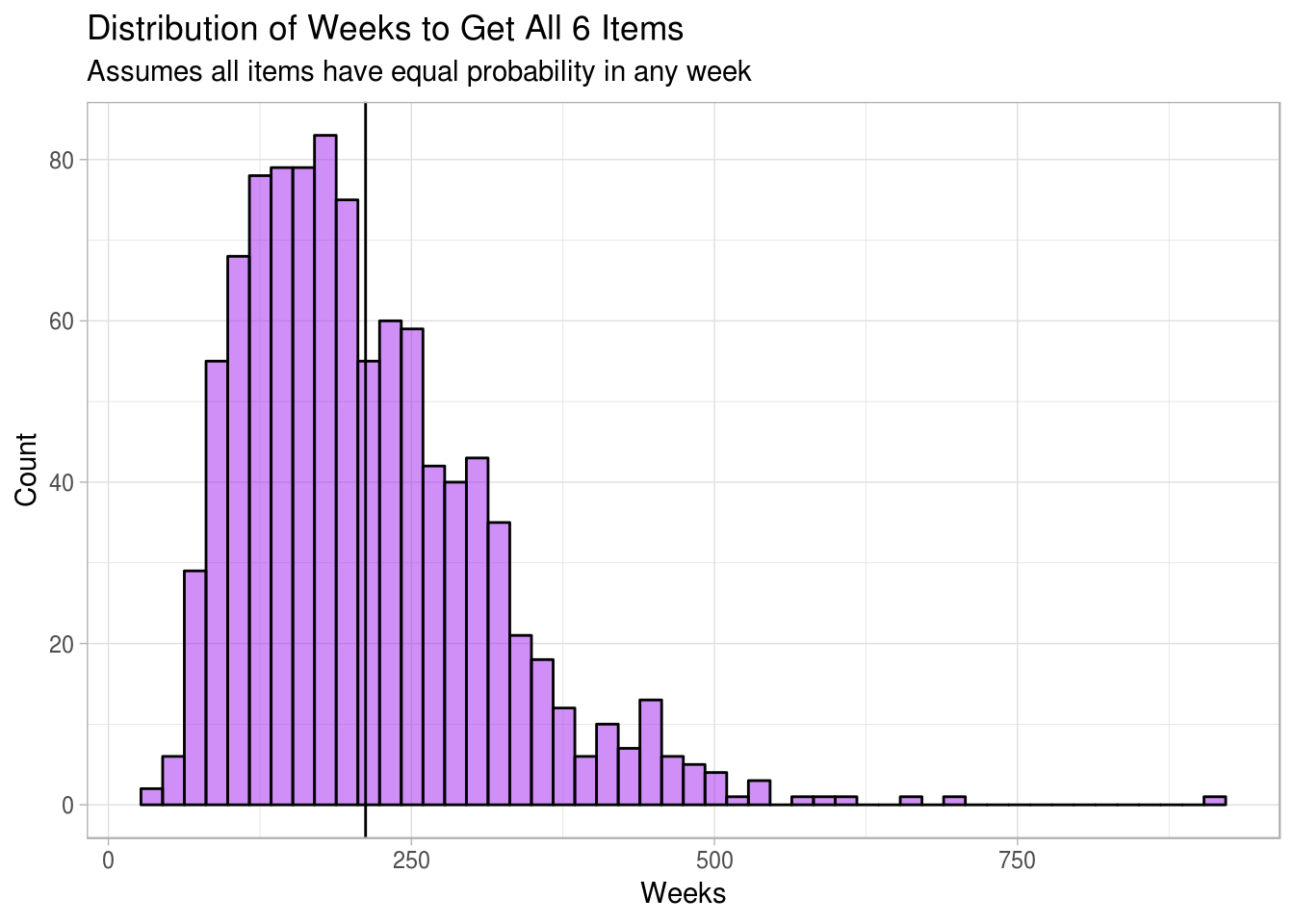

Option 2: I guess I’ll try my luck at the Olympian Gifts

So starting today, January 23, I am going to use all my future Oraculum on the Olympic Gifts, how will I fair? Well, like I said, we have to make assumptions, and one user did 50 pulls from the gifts, and got 8 legendary items. With that we have about a 1 in 6 chance in getting a Legendary Item. We’ve been told that these items do not duplicate, so that helps the odds a little bit. Statistically speaking, I may need 510 pulls to get that whole Athena set. Each pull costs 20 Oraculum, so 510 of them is going to cost the player 10,200 Oraculum. I can consistently acquire about 140 oraculum per week if I’m doing all my dailies and weeklies. Unfortunately, it would two 72 weeks to require 10,200 oraculum at a rate of 140 per week. 72 weeks is 18 months, or a year and a half (which is September 2020). Damnit, this could take weeks or months, unless my numbers are way off, or if I get pretty lucky.

estimated_probability_of_legendary <- 8 / 50

legendary_item_count <- 8 * 7 + 4 # 8 Cosmetic Packs / 4 Weapons

gifts_per_week <- 7

# So I have a binomial disribution with
legendary_items <- list_of_items[list_of_items %in% c(items_wanted, "oth_cosmetic_packs", "legendary_weapons")]

olympian_gifts_needed <- function(item_list, desired_items){
  drawn_items <- vector()
  while(sum(desired_items %in% drawn_items) < 6){
    draw_legendary <- rbinom(1, 1, estimated_probability_of_legendary)
    if(draw_legendary == 1){
      drawn_item <- sample(item_list, 1, replace = FALSE)
    } else {
      drawn_item <- "non_legendary"
    }
    drawn_items <- c(drawn_items, drawn_item)
  }
  return(length(drawn_items))
}

giftboxes_to_athena_items <- map_dbl(1:1000, ~olympian_gifts_needed(legendary_items, items_wanted))
average_weeks_gb <- mean(giftboxes_to_athena_items) / 7

Average Weeks to Items: 131 | Years: 2.52

Probablility it will take less than 1 year: 6.40%

Histogram of Results

ggplot(data.frame(weeks = giftboxes_to_athena_items / 7), aes(x = weeks)) + 
  geom_histogram(bins = 50, fill = "purple", color = "black", alpha = .5) + 
  geom_vline(xintercept = average_weeks_gb) +
  labs(title = "Distribution of Weeks to Get All 6 Items by Giftboxes",
       subtitle = "Assumes 8 out of 50 is the correct probability and all legendary items are equally probable",
       x = "Weeks",
       y = "Count") +
  theme_light()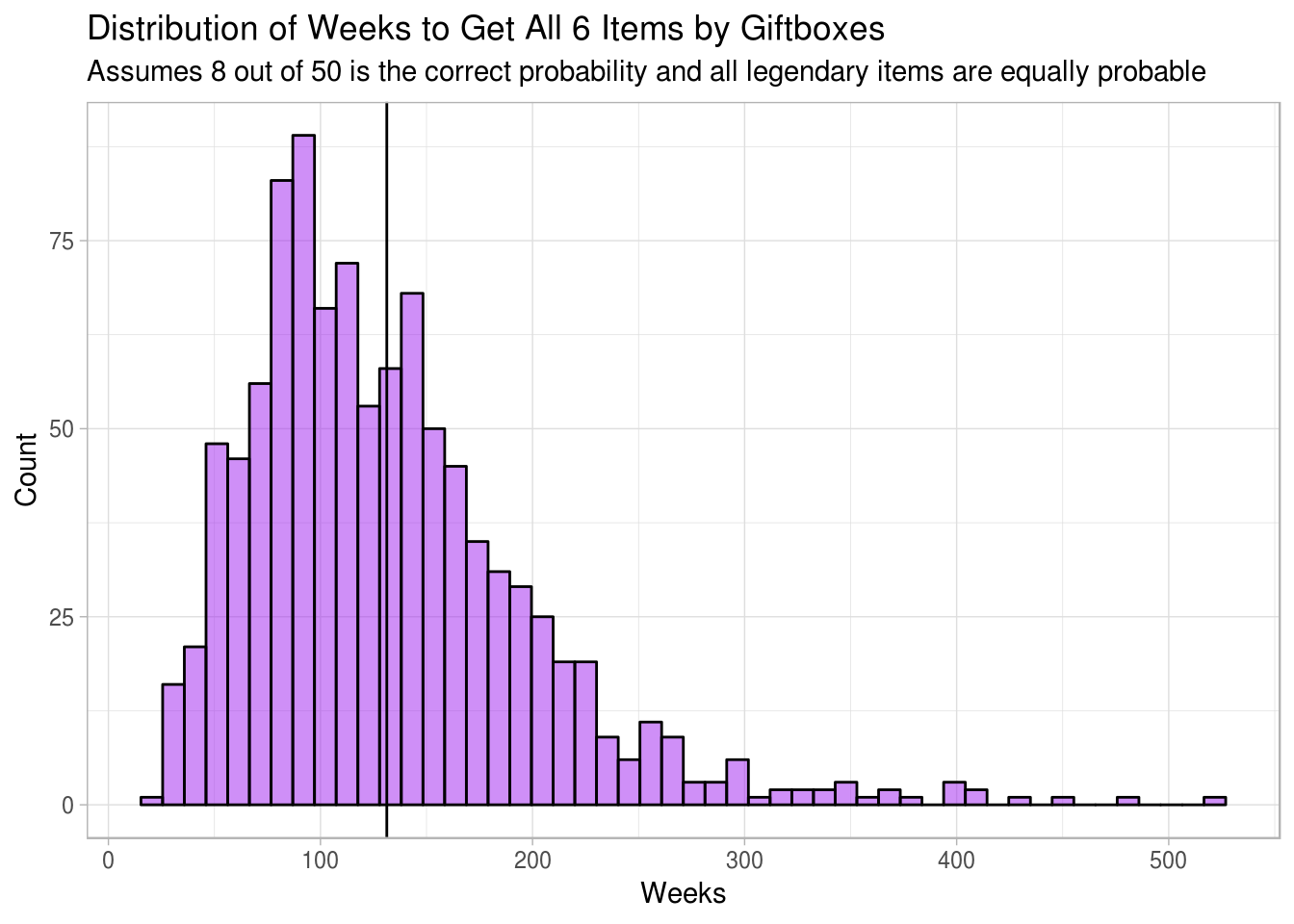

Conclusion

It is significantly more likely that you will achieve all 6 items in less time using option 2 (But it’s still FAR too long!!!). At Minimum Wage in the US ($7.25) and assuming 30min per 20 orachulm. You are valuing these items at $ 3331.19

ggplot(data.frame(weeks = weeks_to_athena_items), aes(x = weeks)) + 
  geom_histogram(bins = 50, fill = "purple", color = "black", alpha = .5) + 
  geom_vline(xintercept = average_weeks) +
  geom_histogram(data = data.frame(weeks = giftboxes_to_athena_items / 7), bins = 50, fill = "blue", color = "black", alpha = .5) + 
  geom_vline(xintercept = average_weeks_gb, color = "red") +
  labs(title = "Distribution of Weeks to Get All 6 Items",
       subtitle = "Assumes all items have equal probability in any week\nOption 1 = Purple, Option 2 = Blue",
       x = "Weeks",
       y = "Count") +
  theme_light()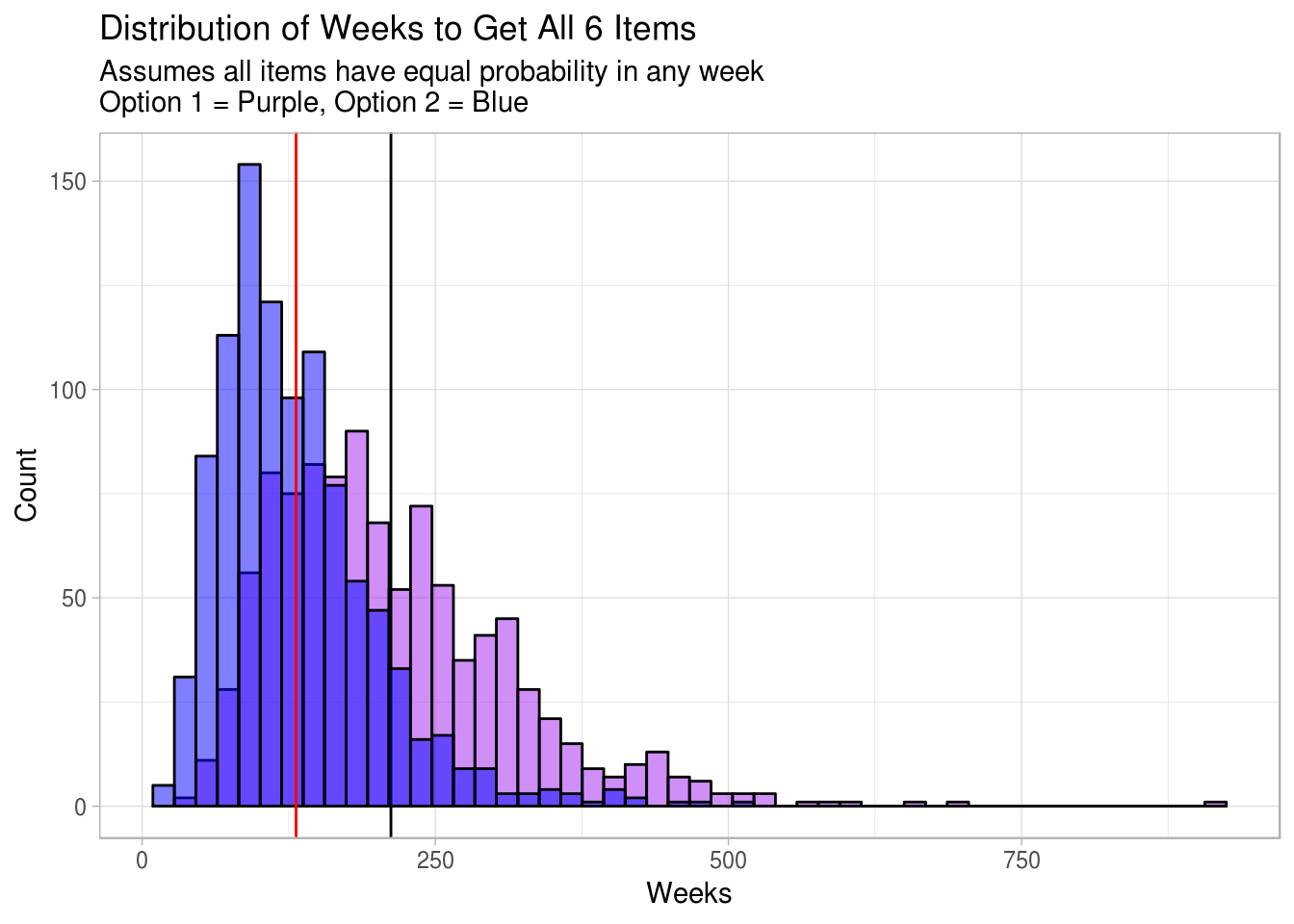

Bonus

What are the odds that option 2 will be faster than option 1?

trials <- tibble(
  weeks = sample(weeks_to_athena_items, size = 1000, replace = TRUE),
  gb_weeks = sample(giftboxes_to_athena_items, size = 1000, replace = TRUE) / 7,
  variance = weeks - gb_weeks
)

probability_op1_gt_op2 <- sum(trials$weeks > trials$gb_weeks) / nrow(trials)
average_variance <- mean(trials$variance)

Probability that option 1 takes longer than option 2: 0.772 Average weeks longer option 1 will take vs. option 2: 87.7981429